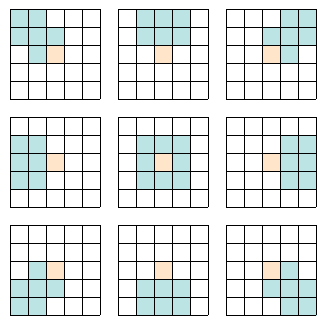
局所近隣平滑化フィルタ
中心のターゲット画素の対し、ターゲット画素の9通りの近傍領域中でその中の画素値の分散が最小になる領域を選び、その平均値をターゲット画素と置き換える。
すると以下のように印象派絵画のとうなフィルタ効果を得ることが出来る。

原画
|

局所近隣平滑化
|
サブルーチン
0:左上、1:上、2:右上、3:右、4:右下、5:下、6:左下、7:左、8:中 のエリアの中からターゲットの画素と最も近い画素で出来ているエリアを見付けるため、RGBを一旦グレイスケールに変換します。
3値のRGBで近似の画素エリアを探すより、1値であるグレイスケールの方が近似エリアを決定し易いからです。
lib/rgb2gray.pm :
1 sub rgb2gray {
2 print "gray scaling\n";
3 for ($j = 0; $j < $size_y; $j++) {
4 for ($i = 0; $i < $size_x; $i++) {
5 @tmp = split /\,/, $org[$i][$j];
6 $rgb2gray = ( ($tmp[0] * 0.299) + ($tmp[1] * 0.578) + ($tmp[2] * 0.114) );
7 $rgb2gray_i = int($rgb2gray);
8 $gray[$i][$j] = $rgb2gray_i;
9 }
10 }
11 }
12 1;
以下が局所近隣平滑化フィルタによってターゲットの画素値を求めるサブルーチンです。
29行目〜67行目でグレイスケールを使って各エリアの平均値とターゲットとの差が最も小さくなるエリアを探しています。
探し出した最も近いエリアによって、その平均値をRGBで計算してターゲットの画素と置き換えるのが69行目以降になっています。
lib/near_part_averaging.pm :
1 sub near_part_averaging {
2
3 ($r[0], $g[0], $b[0] ) = split /\,/, $org[$i-2][$j-2];
4 ($r[1], $g[1], $b[1] ) = split /\,/, $org[$i-1][$j-2];
5 ($r[2], $g[2], $b[2] ) = split /\,/, $org[$i][$j-2];
6 ($r[3], $g[3], $b[3] ) = split /\,/, $org[$i+1][$j-2];
7 ($r[4], $g[4], $b[4] ) = split /\,/, $org[$i+2][$j-2];
8 ($r[5], $g[5], $b[5] ) = split /\,/, $org[$i-2][$j-1];
9 ($r[6], $g[6], $b[6] ) = split /\,/, $org[$i-1][$j-1];
10 ($r[7], $g[7], $b[7] ) = split /\,/, $org[$i][$j-1];
11 ($r[8], $g[8], $b[8] ) = split /\,/, $org[$i+1][$j-1];
12 ($r[9], $g[9], $b[9] ) = split /\,/, $org[$i+2][$j-1];
13 ($r[10], $g[10], $b[10]) = split /\,/, $org[$i-2][$j];
14 ($r[11], $g[11], $b[11]) = split /\,/, $org[$i-1][$j];
15 ($r[12], $g[12], $b[12]) = split /\,/, $org[$i][$j];
16 ($r[13], $g[13], $b[13]) = split /\,/, $org[$i+1][$j];
17 ($r[14], $g[14], $b[14]) = split /\,/, $org[$i+2][$j];
18 ($r[15], $g[15], $b[15]) = split /\,/, $org[$i-2][$j+1];
19 ($r[16], $g[16], $b[16]) = split /\,/, $org[$i-1][$j+1];
20 ($r[17], $g[17], $b[17]) = split /\,/, $org[$i][$j+1];
21 ($r[18], $g[18], $b[18]) = split /\,/, $org[$i+1][$j+1];
22 ($r[19], $g[19], $b[19]) = split /\,/, $org[$i+2][$j+1];
23 ($r[20], $g[20], $b[20]) = split /\,/, $org[$i-2][$j+2];
24 ($r[21], $g[21], $b[21]) = split /\,/, $org[$i-1][$j+2];
25 ($r[22], $g[22], $b[22]) = split /\,/, $org[$i][$j+2];
26 ($r[23], $g[23], $b[23]) = split /\,/, $org[$i+1][$j+2];
27 ($r[24], $g[24], $b[24]) = split /\,/, $org[$i+2][$j+2];
28
29 $ave_area[0] = ( ($gray[$i-2][$j-2] + $gray[$i-1][$j-2] +
30 $gray[$i-2][$j-1] + $gray[$i-1][$j-1] + $gray[$i][$j-1] +
31 $gray[$i-1][$j] + $gray[$i][$j] ) / 7);
32 $ave_area[1] = ( ($gray[$i-1][$j-2] + $gray[$i][$j-2] + $gray[$i+1][$j-2] +
33 $gray[$i-1][$j-1] + $gray[$i][$j-1] + $gray[$i+1][$j-1] +
34 $gray[$i][$j] ) / 7);
35 $ave_area[2] = ( ( $gray[$i+1][$j-2] + $gray[$i+2][$j-2] +
36 $gray[$i][$j-1] + $gray[$i+1][$j-1] + $gray[$i+2][$j-1] +
37 $gray[$i][$j] + $gray[$i+1][$j] ) / 7);
38 $ave_area[3] = ( ( $gray[$i+1][$j-1] + $gray[$i+2][$j-1] +
39 $gray[$i][$j] + $gray[$i+1][$j] + $gray[$i+2][$j] +
40 $gray[$i+1][$j+1] + $gray[$i+2][$j+1] ) / 7);
41 $ave_area[4] = ( ($gray[$i][$j] + $gray[$i+1][$j] +
42 $gray[$i][$j+1] + $gray[$i+1][$j+1] + $gray[$i+2][$j+1] +
43 $gray[$i+1][$j+2] + $gray[$i+2][$j+2] ) / 7);
44 $ave_area[5] = ( ( $gray[$i][$j] +
45 $gray[$i-1][$j+1] + $gray[$i][$j+1] + $gray[$i+1][$j+1] +
46 $gray[$i-1][$j+2] + $gray[$i][$j+2] + $gray[$i+1][$j+2] ) / 7);
47 $ave_area[6] = ( ( $gray[$i-1][$j] + $gray[$i][$j] +
48 $gray[$i-2][$j+1] + $gray[$i-1][$j+1] + $gray[$i][$j+1] +
49 $gray[$i-2][$j+2] + $gray[$i-1][$j+2] ) / 7);
50 $ave_area[7] = ( ($gray[$i-2][$j-1] + $gray[$i-1][$j-1] +
51 $gray[$i-2][$j] + $gray[$i-1][$j] + $gray[$i][$j] +
52 $gray[$i-2][$j+1] + $gray[$i-1][$j+1] ) / 7);
53 $ave_area[8] = ( ($gray[$i-1][$j-1] + $gray[$i][$j-1] + $gray[$i+1][$j-1] +
54 $gray[$i-1][$j] + $gray[$i][$j] + $gray[$i+1][$j] +
55 $gray[$i-1][$j+1] + $gray[$i][$j+1] + $gray[$i+1][$j+1] ) / 9);
56
57 $target = $gray[$i][$j];
58
59 $sub_c = 65535;
60 for ($c = 0; $c < 9; $c++) {
61 $sub = $target - $ave_area[$c];
62 $sub_a = abs($sub);
63 if ($sub_a < $sub_c) {
64 $sub_c = $sub_a;
65 $n = $c;
66 }
67 }
68
69 if ($n == 0) {
70 $r_ave = ( ($r[0] + $r[1] +
71 $r[5] + $r[6] + $r[7] +
72 $r[11] + $r[12] ) / 7);
73 $g_ave = ( ($g[0] + $g[1] +
74 $g[5] + $g[6] + $g[7] +
75 $g[11] + $g[12] ) / 7);
76 $b_ave = ( ($b[0] + $b[1] +
77 $b[5] + $b[6] + $b[7] +
78 $b[11] + $b[12] ) / 7);
79 }
80 if ($n == 1) {
81 $r_ave = ( ($r[1] + $r[2] + $r[3] +
82 $r[6] + $r[7] + $r[8] +
83 $r[12] ) / 7);
84 $g_ave = ( ($g[1] + $g[2] + $g[3] +
85 $g[6] + $g[7] + $g[8] +
86 $g[12] ) / 7);
87 $b_ave = ( ($b[1] + $b[2] + $b[3] +
88 $b[6] + $b[7] + $b[8] +
89 $b[12] ) / 7);
90 }
91 if ($n == 2) {
92 $r_ave = ( ( $r[3] + $r[4] +
93 $r[7] + $r[8] + $r[9] +
94 $r[12] + $r[13] ) / 7);
95 $g_ave = ( ( $g[3] + $g[4] +
96 $g[7] + $g[8] + $g[9] +
97 $g[12] + $g[13] ) / 7);
98 $b_ave = ( ( $b[3] + $b[4] +
99 $b[7] + $b[8] + $b[9] +
100 $b[12] + $b[13] ) / 7);
101 }
102 if ($n == 3) {
103 $r_ave = ( ( $r[8] + $r[9] +
104 $r[12] + $r[13] + $r[14] +
105 $r[18] + $r[19] ) / 7);
106 $g_ave = ( ( $g[8] + $g[9] +
107 $g[12] + $g[13] + $g[14] +
108 $g[18] + $g[19] ) / 7);
109 $b_ave = ( ( $b[8] + $b[9] +
110 $b[12] + $b[13] + $b[14] +
111 $b[18] + $b[19] ) / 7);
112 }
113 if ($n == 4) {
114 $r_ave = ( ($r[12] + $r[13] +
115 $r[17] + $r[18] + $r[19] +
116 $r[23] + $r[24] ) / 7);
117 $g_ave = ( ($g[12] + $g[13] +
118 $g[17] + $g[18] + $g[19] +
119 $g[23] + $g[24] ) / 7);
120 $b_ave = ( ($b[12] + $b[13] +
121 $b[17] + $b[18] + $b[19] +
122 $b[23] + $b[24] ) / 7);
123 }
124 if ($n == 5) {
125 $r_ave = ( ( $r[12] +
126 $r[16] + $r[17] + $r[18] +
127 $r[21] + $r[22] + $r[23] ) / 7);
128 $g_ave = ( ( $g[12] +
129 $g[16] + $g[17] + $g[18] +
130 $g[21] + $g[22] + $g[23] ) / 7);
131 $b_ave = ( ( $b[12] +
132 $b[16] + $b[17] + $b[18] +
133 $b[21] + $b[22] + $b[23] ) / 7);
134 }
135 if ($n == 6) {
136 $r_ave = ( ( $r[11] + $r[12] +
137 $r[15] + $r[16] + $r[17] +
138 $r[20] + $r[21] ) / 7);
139 $g_ave = ( ( $g[11] + $g[12] +
140 $g[15] + $g[16] + $g[17] +
141 $g[20] + $g[21] ) / 7);
142 $b_ave = ( ( $b[11] + $b[12] +
143 $b[15] + $b[16] + $b[17] +
144 $b[20] + $b[21] ) / 7);
145 }
146 if ($n == 7) {
147 $r_ave = ( ($r[5] + $r[6] +
148 $r[10] + $r[11] + $r[12] +
149 $r[15] + $r[16] ) / 7);
150 $g_ave = ( ($g[5] + $g[6] +
151 $g[10] + $g[11] + $g[12] +
152 $g[15] + $g[16] ) / 7);
153 $b_ave = ( ($b[5] + $b[6] +
154 $b[10] + $b[11] + $b[12] +
155 $b[15] + $b[16] ) / 7);
156 }
157 if ($n == 8) {
158 $r_ave = ( ($r[6] + $r[7] + $r[8] +
159 $r[11] + $r[12] + $r[13] +
160 $r[16] + $r[17] + $r[18] ) / 9);
161 $g_ave = ( ($g[6] + $g[7] + $g[8] +
162 $g[11] + $g[12] + $g[13] +
163 $g[16] + $g[17] + $g[18] ) / 9);
164 $b_ave = ( ($b[6] + $b[7] + $b[8] +
165 $b[11] + $b[12] + $b[13] +
166 $b[16] + $b[17] + $b[18] ) / 9);
167 }
168 $r_ave_i = int($r_ave);
169 $g_ave_i = int($g_ave);
170 $b_ave_i = int($b_ave);
171 $color = "$r_ave_i" . ',' . "$g_ave_i" . ',' . "$b_ave_i";
172 return $color;
173 }
174
175 1;
親プログラム
上の局所近隣平滑化フィルタのサブルーチンを使って、実際の画像処理をするのが以下のプログラムです。前ページの鮮鋭化フィルタと同じ構造で、サブルーチンとして sharping となっていた箇所を near_part_averaging に書き換えただけです。
near_part_averaging.pl :
1 #!/usr/bin/perl
2
3 use Getopt::Long;
4
5 use lib '/home/user/Lab/ImageProcessing/Perl/lib';
6 require read_jpg;
7 require rgb2gray;
8 require near_part_averaging;
9 require apply_area;
10
11 sub print_synopsis {
12 print "Options : \n";
13 print " --input_file : \n";
14 print " input original file name.\n";
15 print " --shape : \n";
16 print " shape of filer area either s as square or c as circle.\n";
17 print " if not defined, n is set to this option.\n";
18 print " --center : \n";
19 print " center position x,y\n";
20 print " if not defined, 960,540 is set to this option.\n";
21 print " --volume : \n";
22 print " filter area size. distance from center.\n";
23 print " if not defined, 1400 is set to this option.\n";
24 print " --xratio : \n";
25 print " ratio of x size of filter area\n";
26 print " if not defined, 1 is set to this option.\n";
27 print " --eio : \n";
28 print " filter effective area either i as inside or o as outside.\n";
29 print " if not defined, o is set to this option.\n";
30 }
31
32 GetOptions(
33 'input_file=s' => \$in_file,
34 'shape=s' => \$in_shape,
35 'center=s' => \$in_center,
36 'volume=i' => \$in_volume,
37 'xratio=f' => \$in_xratio,
38 'eio=s' => \$in_eio,
39 'nodisp' => \$in_nodisp,
40 );
41
42 if (!defined($in_file)) {
43 print "##ERROR## input file has not been defined\n";
44 &print_synopsis;
45 exit;
46 }
47
48 if (!defined($in_shape)) {
49 print "shape of averaging area is not defined\n";
50 $shape = 'n';
51 } else {
52 if (!(($in_shape eq "s")||($in_shape eq "c"))) {
53 print "##ERROR## invalid shape is defined. define s as square or c as circle\n";
54 exit;
55 } else {
56 $shape = $in_shape;
57 }
58 }
59
60 if (!defined($in_center)) {
61 $center_x = 960;
62 $center_y = 540;
63 } else {
64 @tmp_center = split /\,/, $in_center;
65 $center_x = $tmp_center[0];
66 $center_y = $tmp_center[1];
67 }
68
69 if (!defined($in_volume)) {
70 $volume = 1400;
71 } else {
72 $volume = $in_volume;
73 }
74
75 if (!defined($in_xratio)) {
76 $xratio = 1;
77 } else {
78 $xratio = $in_xratio;
79 }
80
81 if (!defined($in_eio)) {
82 $eio = 'o';
83 } else {
84 if (!(($in_eio eq "i")||($in_eio eq "o"))) {
85 print "##ERROR## invalid effective area is defined. define i as inside or o as outside\n";
86 exit;
87 } else {
88 $eio = $in_eio;
89 }
90 }
91
92 &read_jpg($in_file);
93
94 &rgb2gray();
95
96 print "near averaging\n";
97 for ($j = 0; $j < $size_y; $j++) {
98 for ($i = 0; $i < $size_x; $i++) {
99 if (($i < 2) || ($i >= ($size_x - 2)) || ($j < 2) || ($j >= ($size_y - 2))) {
100 $near_part_average[$i][$j] = $org[$i][$j];
101 } else {
102 if ($shape eq "n") {
103 $near_part_average[$i][$j] = &near_part_averaging;
104 } else {
105 $apply_calc = &apply_area($shape, $center_x, $center_y, $volume, $xratio, $eio, $i, $j);
106 if ($apply_calc == 1) {
107 $near_part_average[$i][$j] = &near_part_averaging;
108 } else {
109 $near_part_average[$i][$j] = $org[$i][$j];
110 }
111 }
112 }
113 }
114 }
115
116 print "output text file\n";
117 open(OUT_TEXT, ">", "../Temp/near_part_averaging.txt") or die
"##ERROR## Could not open output file : ../Temp/near_part_averaging.txt";
118 print OUT_TEXT "$header\n";
119 for ($y = 0; $y < $size_y; $y++) {
120 for ($x = 0; $x < $size_x; $x++) {
121 $state = "$x" . ',' . "$y" . ': ' . '(' . "$near_part_average[$x][$y]" . ')';
122 print OUT_TEXT "$state\n";
123 }
124 }
125 close OUT_TEXT;
126
127 print "convert text to jpeg\n";
128 `convert ../Temp/near_part_averaging.txt ../Temp/near_part_averaging.jpg`;
129
130 if (!defined($in_nodisp)) {
131 if ( ($size_x <= 1920) && ($size_y <= 1080) ) {
132 print "display\n";
133 `display ../Temp/near_part_averaging.jpg`;
134 } else {
135 print "jpeg size is too large, open with gimp\n";
136 }
137 }
138
親プログラムについての解説は、前ページの鮮鋭化フィルタと同じですので省略します。


|

自己紹介
50才になる半導体エンジニアです。
大学で電子電気工学を学び、1990年にその分野のまま就職。ASICやマイコンの設計を長く続けてきましたが20年も同じ分野にいると業態も衰退したり変化するもので退職し、今は外資のIT系会社に再就職して設計請負業をやっております。
お問い合わせは
nakata.xianzhi@outlook.com


Linux と 小ネタ
デジタル回路設計
海外駐在後記











|